Del 3 i ”Tänkarskola för beslutsfattare” bygger vidare på ”#2 Korrelation vs. kausalitet” och handlar om det mycket viktiga fenomenet ”regression mot medelvärdet”.
Det statistiska begreppet ”regression” betyder i det här sammanhanget ungefär ”återgång”, och det går inte att nog poängtera hur viktig en förståelse för fenomenet är inom i princip alla typer av verksamheter – och för att bli lite dramatisk: för förståelsen av hela vår tillvaro. Sist i inlägget finns också ett isande exempel på när det bokstavligt talat har betydelse för liv och död – avrättning eller inte?
Att som beslutsfattare känna till att fenomenet finns och dyker upp lite överallt är ett stort steg på vägen att fatta bättre beslut, och att även kunna utvärdera resultatet av olika satsningar betydligt bättre.
Vardagsexempel
Ex 1. Du är rektor på en skola och bestämmer att en grupp pedagoger ska göra en extra utbildningssatsning på de 10 % av eleverna som misslyckats mest på ett nationellt prov. Satsningen görs, eleverna får göra ett nytt, jämförbart prov, och gruppens medelresultat blir nu bättre. Går det då att säga att utbildningssatsningen har haft effekt?
Ex 2. Du är HR-chef på ett företag och genomför i samarbete med företagshälsovården en ganska kostsam friskvårdssatsning för att förbättra hälsan hos en grupp på 30 anställda, som haft högst sjukfrånvaro per månad av företagets samtliga 150 anställda. Två månader senare – efter diverse stödåtgärder – noteras att samma 30 individer under den senaste månaden haft en genomsnittligt lägre sjukfrånvaro. Går det då att säga att minskningen i sjukfrånvaro beror på den särskilda satsningen?
I två sådana här enkla och vanliga exempel skulle nog många säga att förbättringarna beror på satsningarna. Problemet är att det inte säkert går att säga att så är fallet – inte utan att man dessutom har likvärdiga kontrollgrupper som inte får ta del av satsningarna.
Till detta måste också läggas risken för s.k. bekräftelsebias (confirmation bias). Både som rektor och som HR-chef VILL du antagligen att satsningarna ska visa på en effekt – du vill ju gärna framstå som handlingskraftig, och pengarna har säkert tagits ur en hårt slimmad budget.
Naturliga förändringar – och slumpen
Men vad kan då ligga bakom förbättringarna om inte de specifika satsningarna?
I det första exemplet kanske omständigheterna helt enkelt är gynnsammare vid det andra provtillfället: dagsformen hos en del av eleverna kanske är bättre, vissa av eleverna kanske har bättre tur med frågorna och okända, slumpmässiga faktorer är kanske i högre grad till vissa elevers fördel. Detta sammanlagt gör att eleverna som gjorde dåligt ifrån sig på det första provet sannolikt, utan några insatser alls, i genomsnitt gör bättre ifrån sig på det andra provet.
I det andra exemplet är det på samma sätt högst möjligt att det förbättrade genomsnittet för den utvalda gruppen kommer av diverse naturliga orsaker – t.ex. övergående stress- eller sömnproblem, gynnsam påverkan av årstid och solljus eller att någon typ av somatisk eller psykisk åkomma har förbättrats spontant, eller till och med läkt ut. På två månader hinner många individer, utan några speciella insatser, återhämta sig en hel del från vanliga och övergående dippar i hälsa och välmående. Alla de här effekterna kan ligga bakom att gruppens genomsnittliga sjukfrånvaro gått ner.
Båda exemplen illustrerar fenomenet att avvikelser från ett medelvärde hos en grupp rent statistiskt tenderar att normaliseras en del av naturliga orsaker (inklusive variationer vad gäller tur och ”slump”), så att det sker en ”regression mot medelvärdet”, RMM.
Ju större avvikelse från medelvärdet vid första tillfället desto normalare gruppsnitt vid andra tillfället. Det är därför det kan vara extra lömskt med olika satsningar baserade på selektiva urval från s.k. ”extremgrupper”.
Andra exempel
Fenomenet RMM uppträder i vitt skilda sammanhang:
- Idrottare som presterat exceptionellt bra under en säsong, med en serie resultat över genomsnittet, kommer sannolikt att prestera sämre under nästa säsong – även om träningen ligger kvar på samma nivå.
- Ett företag som haft ett ovanligt dåligt kvartalsresultat (en sammanvägning av olika delvärden) kommer sannolikt att få ett bättre resultat under nästa kvartal – även utan att några särskilda åtgärder satts in.
- Föräldrar med en längd över genomsnittet kommer sannolikt att få barn vars längd ligger närmare genomsnittet.
Och så vidare.
Lägg märke till att jag skriver ”sannolikt”. I varje enskilt fall finns det nämligen alltid en viss statistisk möjlighet att värde nr 2 fortfarande avviker mycket från medelvärdet. Det är därför viktigt att påpeka att RMM i statistiken är ett fenomen strikt på gruppnivå, inte på individnivå. Det är gruppens medelvärde som rör sig mot mitten. Och som sagt: ju mer avvikande grupp man väljer att studera desto större blir RMM-effekten.
När jag själv gick på läkarutbildningen i Lund en gång i tiden fick vi inte lära oss något om RMM, och ändå är det ett oerhört viktigt fenomen att känna till inom sjukvården. Här är en lättbegriplig och viktig artikel från Läkartidningen (2006), som tar upp fenomenet i samband med passageröntgen och s.k. ileus (”tarmvred” i dagligt tal).
Kontrollgrupper
Som jag nämnde ovan är en viktig metod för att hantera och bedöma RMM-effekten att använda kontrollgrupper. Slår man utan kontrollgrupper fast att förbättringarna beror på satsningarna gör man sig med stor sannolikhet skyldig till s.k. ”regression fallacy”.
En första grundregel är att kontrollgrupperna måste likna undersökningsgrupperna så mycket som möjligt. En andra grundregel är att inte använda för små grupper, eftersom det gör analyserna mer osäkra. Följer man dessa två grundregler ökar möjligheterna att göra korrekta analyser av satsningarna.
Om grupperna med elever eller anställda i de två exemplen ovan uppfyller kraven för kontrollgrupper kan man t.ex. i en första testsatsning låta hälften få stödinsatser och andra hälften inga insatser alls. Därefter fastställer man om det finns någon statistiskt signifikant skillnad mellan grupperna. Finns det en sådan skillnad kan den sannolikt, men aldrig 100-procentigt, förklaras av stödåtgärderna.
Med tanke på alla fällor som lurar i ett sådant här upplägg bör det därför endast iscensättas om de ansvariga för åtgärderna behärskar statistiska metoder väl. Gör man inte det är det bäst att ta hjälp från professionellt håll med både upplägg och utvärdering.
Det är ju knappast försvarbart att spendera tid och pengar på en satsning som inte går att utvärdera ordentligt, och som riskerar att antingen bara bli en medioker engångsinsats eller ännu värre: bli en återkommande men verkningslös ”modell”, för att visa att man satsar på åtgärder för svaga grupper.
Man bör alltså först genomföra en adekvat testsatsning som kan utvärderas ordentligt. Faller den väl ut kan upplägget/metoden sedan på ett försvarbart sätt användas upprepade gånger.
Beröm och kritik
Fenomenet att dåliga prestationer normalt följs av bättre och att bra prestationer följs av sämre får ibland det paradoxala till följd att kritik och bestraffningar efter sämre prestationer kan tyckas leda till förbättringar, medan beröm och uppmuntran efter goda insatser istället kan tyckas ge sämre resultat. Det går emot mängder av forskning som visar på motsatsen: att träning av olika färdigheter fungerar bättre om man belönar de goda prestationerna, istället för att man bestraffar misstagen.
I den här videon, från den utmärkta Youtube-kanalen Veritasium, tar Derek Muller upp RMM. Han baserar det mesta i klippet på vad nobelpristagaren Daniel Kahneman skriver om fenomenet i sin bästsäljande bok ”Tänka, snabbt och långsamt” (Thinking, fast and slow, 2011). Om du har den i bokhyllan – läs kapitel 17!
I kapitlet om regression mot medelvärdet skriver Kahneman följande, i ett resonemang kring professionella golfspelares insatser under några dagars tävling:
Framgång = begåvning + tur
Stor framgång = lite mer begåvning + mycket tur
Rimligen borde väl här begåvning kombineras med träning också, men poängen med hela resonemanget är: för alla dem som vill tro att stora framgångar enbart beror på exceptionell begåvning och optimala personlighetsdrag (ihop med hårt arbete) är det dags att tänka om.
Någon enstaka gång kan det förstås vara så, men i den överväldigande delen av alla fall av extra stor framgång är den sannolikaste bakomliggande orsaken också en extra stor portion tur.
Till sist en mycket viktig sak att komma ihåg:
Fenomenet med RMM säger ingenting alls om något kausalt samband (orsakssamband, se blogginlägg #2), för skiftningarna mellan bra och dåliga resultat.
Men eftersom den mänskliga hjärnan tolkar in kausala samband lite varstans och när som helst (se blogginlägg #1 om kausaldriften) fyller vi gärna i och hittar på olika förklaringar till RMM.
Hjärnan är helt enkelt mycket bättre på att hitta på falska orsakssamband, och skapa historier som bekräftar dem, än den är på att objektivt förstå statistik.
Alltså: regression mot medelvärdet har en förklaring, men ingen orsak!
“Regression toward the mean is not based on cause and effect, but rather on random error in a natural distribution around a mean.” (Wikipedia)
Efter den här genomgången rekommenderar jag den som vill veta mer om RMM, inklusive lite historik, att läsa vad Wikipedia skriver. (Obs! Lång text.)
Överkurs
För att anknyta till mitt förra inlägg ”#2 Korrelation vs. kausalitet”, så kan man rent matematiskt förklara regression mot medelvärdet med hjälp av begreppet korrelation.
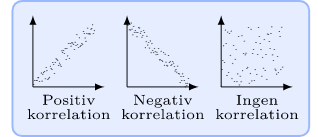
Som jag förklarar där uttrycks styrkan och riktningen i korrelationen mellan variablerna med hjälp av en korrelationskoefficient, r, som varierar mellan +1 (100% positiv korrelation) och -1 (100% negativ korrelation).
+1 och -1 förekommer väldigt sällan, utan korrelationen ligger oftast någonstans däremellan. Detta innebär då att det finns något annat än just de specifika variablerna man undersöker som också har betydelse för hur sambandet och korrelationen ser ut.
Det går att uttrycka så här: om korrelationen mellan två variabler inte är 100-procentig går det inte att undvika ”regression mot medelvärdet”. Det är så att säga matematiskt inbyggt i sambandet.
För den som varken räds regressions- eller vektoranalys ger den här (långa) Youtube-videon en mycket grundlig genomgång av matematiken bakom ”regression toward the mean”. Den mynnar ut i en sammanfattning av alltihop med den här eleganta formeln:
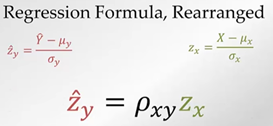
Kommentarerna till videon är intressanta. Där framgår bl.a. varför videon gjordes, och varför den innehåller så mycket matematik och resonemang kring just IQ-nivåer. Här handlar en förståelse för RMM bokstavligt talat om liv och död – avrättning eller inte?
”One of the reasons I included so much mathematical detail was that I made the video for a team of lawyers defending a man with an intellectual disability on death row.”
(Joel Schneider)
Tack för uppmärksamheten!